Framatophe   ... Blog 

Accueil  |  Publis | Je | 🐳 | ☕ | 📩 | 🔊

Révolutions informatiques : algorithmes et pouvoirs

☙  Posté le 24-06-2015  | ⏱ 22 minutes  | ✔ 4579 mots
✎  Christophe Masutti

Il y a 45 ans, avec l’arrivée en masse de l’informatique et du micro-ordinateur dans les entreprises, les foyers français, et à peu près tous les secteurs de l'économie, la notion de « Révolution Informatique » occupait le thème d’un des célèbres colloques de Cerisy-la-Salle du 10 au 20 juillet 1970.

Les actes de ce colloque, aujourd’hui indisponibles, méritent toutefois d'être lus aujourd’hui à bien des titres. Tout particulièrement à l’heure où notre gouvernement est en passe de voter un texte de surveillance de masse de nos outils de communication. En effet, en automatisant les tâches de surveillance par des algorithmes, ce qui revient à surveiller tout le monde pour faire un tri ensuite, il se développe actuellement une sorte d’accomplissement d’un pouvoir techniciste au prix d’une dépossession du peuple des instruments de la circulation de l’information, au fondement de la démocratie. Or, c’est étonnement un axe de lecture tout à fait intéressant des actes du colloque de ce mois de juillet 1970…

Deux textes en particulier méritent un détour. Le premier explique la notion d’algorithme. Un peu ardu à certains endroits, son auteur Jacques Riguet est néanmoins fort synthétique, et montre qu’en réalité ce qu’on appelle un algorithme est loin de mériter un traitement aussi désinvolte que celui que lui réservent nos responsables politiques du moment, puisqu’il s’agit de définir de l’imprécis par un choix d'éléments précis. Surveiller la population par des algorithmes suppose donc de manière systématique de l’imprécision et par conséquent nécessite d’expliquer précisément la classe des éléments choisis en fonction du but poursuivi. Si l’objectif est trop large, les algorithmes ne peuvent être précis : la Loi Renseignement ne peut donc pas concilier les deux, cqfd.

Le second texte est de la plume de Louis Pouzin, connu comme l’un des pionniers des recherches sur le temps partagé (voir sa fiche Wikipédia) aux sources de notre Internet d’aujourd’hui. Son texte porte sur les aspects technocratiques de l’informatique utilisée comme instrument décisionnaire. Loin de relayer des craintes infondées et anti-progressistes, ils soulève néanmoins quelques questions fort pertinentes sur le rapport qu’entretien le pouvoir avec le traitement informatique de l’information. Car en effet, déjà l’Internet balbutiant montrait qu’il pouvait être un extraordinaire outil de partage de l’information et par conséquent un outil majeur du dialogue démocratique. Si la génération des hommes politiques d’alors n'était pas encore prête à amortir cette révolution informatique naissante, il était tout à fait pertinent de s’interroger un peu sur l’avenir. Et ce n’est pas innocemment que l’auteur conclu en ces termes : « L’invocation de l’ordinateur est un camouflage commode pour l’accomplissement de politiques occultes. »

Je livre donc ces deux textes ci-dessous. J’espère que les responsables des publications du Centre Culturel International de Cerisy ne m’en voudront pas d’outrepasser ici le droit de citation pour aller un peu plus loin : le livre n'étant plus édité, je donne en quelque sorte une seconde vie à ces deux textes :

Révolutions informatiques

Titre : Révolutions informatiques
Direction : François Le Lionnais
Éditeur : Union Générale d'Éditions
Collection : 10/18
Année de publication : 1972
Année du colloque : 1970
Table des matières

Section : Naissance et développement de l’informatique

Dimanche 12 juillet 1970 (après-midi), intervention de Jacques Riguet, Professeur à l’Université de Limoges (pp. 89-97)

La notion d'algorithme

Le mot « algorithme » a une signification voisine de celle des mots « recette », « procédé », « méthode », « technique », « routine ».

La notion d’algorithme est une notion intuitive, donc essentiellement imprécise, tout comme l’est, par exemple, la notion de courbe en géométrie. Un thème fondamental de la recherche mathématique consiste à tenter de donner des définitions précises d’un concept imprécis, le succès de la tentative étant de plus en plus assuré au fur et à mesure que l’on parvient à prouver que les définitions proposées sont équivalentes. Un exemple célèbre de ce thème de recherche nous est fourni par le résultat obtenu par Hahn et Mazur-Kiewicz en 1914 : la notion d’espace métrique compact connexe localement connexe et la notion d’image par une application continue d’un segment dans un espace séparé sont équivalentes et constituent donc une définition précise de la notion intuitive de courbe.

Nous verrons plus loin que les logiciens contemporains sont parvenus à démontrer l'équivalence de diverses notions précises susceptibles de recouvrir la notion intuitive d’algorithme. Mais, pour le moment, il nous faut proposer une définition de celle-ci. La voici :

On appelle algorithme une méthode générale pour la résolution d'une classe de problèmes, fixée en tous ses détails par des règles dépourvues de sens, de façon à ce qu'on puisse l'appliquer sans avoir à la comprendre.

Il convient de donner de suite un exemple :

L’algorithme d’Euclide pour la recherche du P.G.C.D. La classe de problèmes auxquels il s’applique est définie ainsi : étant donné deux entiers positifs m et n, trouver leur plus grand commun diviseur (c’est-à-dire le plus grand entier positif qui divise à la fois m et n).

pgcd

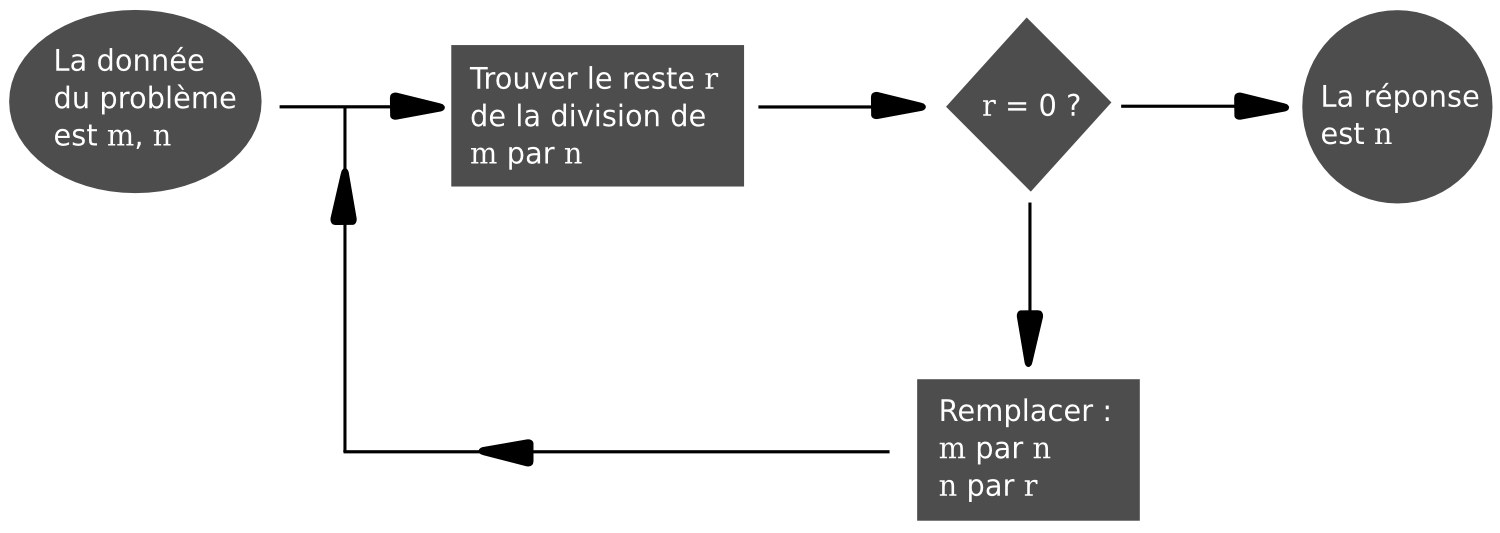
  1. Diviser m par n. Soit r le reste (on a 0≤r<n) ;
  2. Si r=0, l'algorithme est terminé, la réponse est n ;
  3. Si r≠0 remplacer m par n, n par r et opérer comme en 1.

Voir ci-dessous l’exemple d’application de l’algorithme aux nombres m=165 et n=616

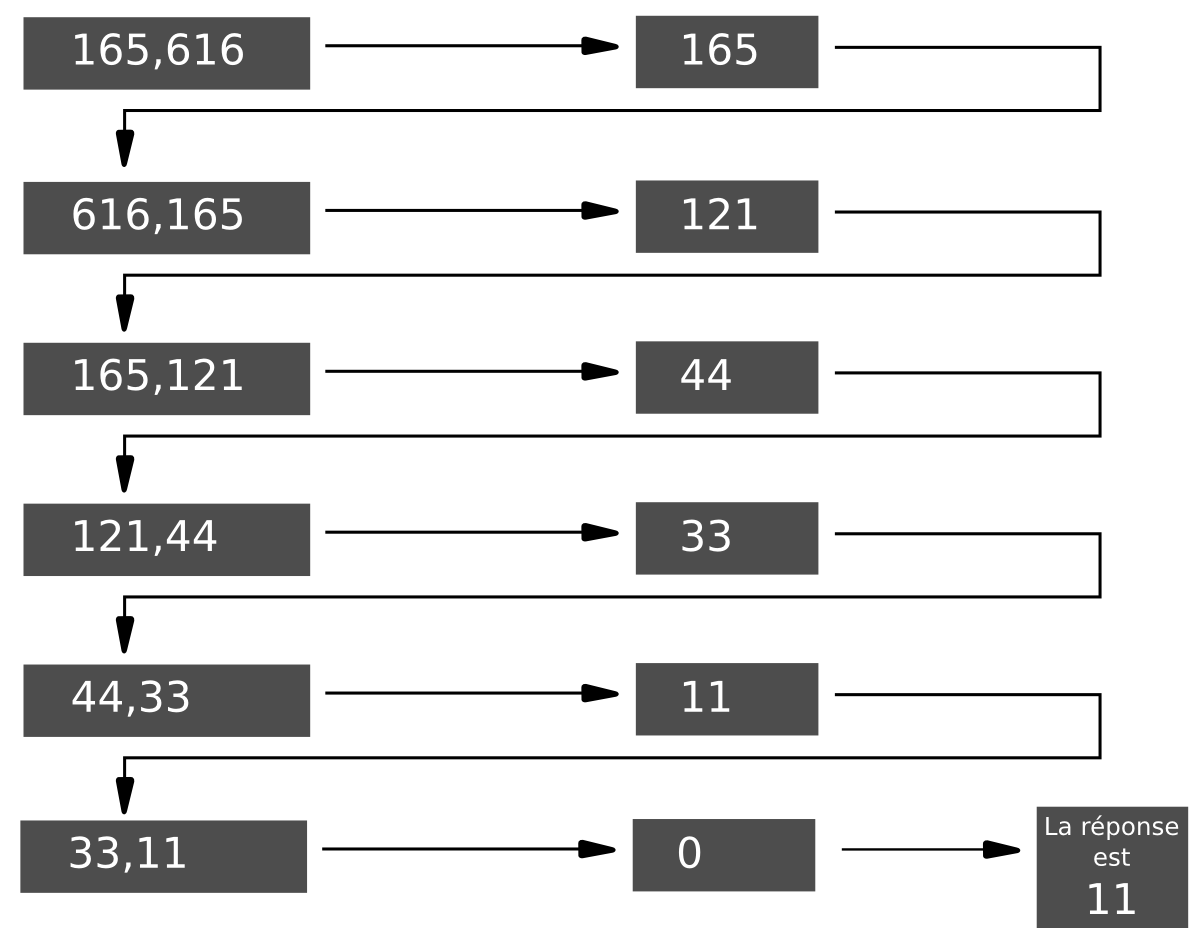
Déjà les arabes, sous l’influence des hindous, avaient développé des algorithmes.

Le mot « algorithme » lui-même est dérivé du nom de l’auteur d’un texte arabe : Abu Ja’far Mohammed ibn Mûsâ al-Khowârizmî (vers 825) (c’est-à-dire père de Ja’far, Mohammed, fils de Moïse, natif de Khowârîzm) (Khowârîzm est aujourd’hui la petite ville de Khiva en U.R.S.S.). Le mot algèbre lui-même est dérivé du titre de son livre « Kitab al jabr w’almuqabala » (Règles de restauration et de réduction) bien que le livre ne soit pas très algébrique.

Vers 1300, l’espagnol Raymond Lulle reprend les méthodes introduites par les arabes pour l'édification de son « Ars magna » qui devait être une méthode générale pour découvrir « toutes les vérités » à partir de combinaisons. Et c’est comme contribution à l'ars magna que Cardan publiera quelques deux cents ans plus tard ses formules et algorithmes algébriques. La « méthode » de Descartes a essentiellement pour but de permettre la résolution des problèmes de géométrie grâce à leur traduction algébrique et au traitement algorithmique de cette traduction (Descartes pensait manifestement que tous les problèmes algébriques pouvaient être traités algorithmiquement, ce qui s’est révélé faux par la suite). Leibniz a rêvé d’une « caractéristique universelle » permettant de résoudre tous les problèmes. Il est encore plus manifeste chez lui que chez Lulle que celle-ci doit être mise en œuvre par une machine. Il est l’un des premiers à construire une machine à calculer.

Reprenons maintenant la définition de la notion d’algorithme que nous avons posée au début et précisons-en quelques points.

  1. Un algorithme étant apte à la résolution d'une classe de problèmes, son énoncé doit comporter une description plus ou moins symbolique des données caractérisant cette classe (nous dirons que c'est son entrée ou sa source) et également une description plus ou moins symbolique des solutions de ces problèmes (nous dirons que c'est sa sortie ou son but). Par exemple, l'algorithme d'Euclide a pour source l'ensemble des couples d'entiers positifs non nuls (en écriture de base 10 par exemple) et pour but l'ensemble des entiers positifs non nuls.
  2. Un algorithme doit être fixé en tous ses détails. En particulier :
    • les instructions doivent être d'une précision absolue. Une recette de cuisine bien qu'ayant une entrée (les « matières premières » : œufs, beurre, farine, etc.) et une sortie (gâteau d'anniversaire, etc.) ne peut être considérée comme un algorithme si elle comporte des instructions telles que « ajouter une pincée de sel » ;
    • l'ordre d'application des règles doit être donné sans ambiguïté. Un organigramme constitué de boîtes d'instructions et d'aiguillages en rendra encore mieux compte que le langage ordinaire.
  3. Un algorithme doit être effectif : cela signifie que chacune de ses règles est suffisamment simple pour pouvoir être effectuée en un temps fini par un homme peut-être stupide et dépourvu de toute imagination mais parfaitement obéissant, muni d'un crayon (inusable) et d'un papier (indéfiniment prolongeable) et qui opère de façon purement mécanique sans réfléchir et sans se soucier du sens que pourraient avoir ces règles1.

On remarquera qu’en quelque sorte 3. implique 2. : si le conducteur de l’algorithme est dépourvu d’imagination, il sera incapable de suppléer au manque de précision ou à la défaillance d’une instruction.

On remarquera aussi que le conducteur de l’algorithme est censé effectuer ses calculs pas à pas, de manière discrète et déterministe sans avoir recours à des méthodes continues ou analogiques ou stochastiques.

Un algorithme ayant une source (classe de problèmes) et un but (énoncé de la solution) définit par là même une fonction que l’on dit calculable par l’algorithme. Par exemple, la fonction f définie par : « quels que soient les entiers positifs non nuls x,y:f(x,y)=P.G.C.D. de x et de y » est une fonction calculable par l’algorithme d’Euclide.

Il est très facile de se rendre compte que, si une fonction est calculable par un algorithme, il en existe d’autres grâce auxquels elle est également calculable. Et c’est un problème important que d’avoir des critères permettant de choisir, parmi ceux-ci, ceux qui réalisent les meilleures performances du point de vue économie de temps ou du point de vue d’autres critères tels que : facilité d’adaptation aux ordinateurs, simplicité, élégance… Il y a là un domaine nouveau à explorer : celui de l’optimalisation des algorithmes.

Il est moins facile de se rendre compte qu’il existe des fonctions qui ne sont pas calculables par un algorithme. Et c'était même là le sentiment erroné des mathématiciens des siècles précédents. Même la découverte de démonstration d’impossibilité de résolution de certains problèmes (par exemple : construction géométrique à l’aide de la règle et du compas, résolubilité des équations algébriques par radicaux) n’influença guère les mathématiciens dans cette croyance, car il s’agissait de la non résolubilité de problèmes grâce à des moyens déterminés mais non d’une impossibilité générale. La démonstration de l’existence de fonctions qui ne sont pas calculables par un algorithme suppose que l’on a défini de façon précise le concept d’algorithme puisqu’une telle démonstration fait appel à la classe de tous les algorithmes. En fait, le problème de la définition précise de la notion d’algorithme est lié étroitement à celui de la définition précise de fonction calculable : une fonction est calculable s’il existe un algorithme permettant de calculer f(n) quel que soit l’entier n. Réciproquement, la méthode d’arithmétisation de Gödel des mots d’une syntaxe permet de déduire le concept d’algorithme de celui de fonction calculable.

Et, historiquement, les recherches de définitions précises ont porté d’abord sur la notion de fonction calculable avec Skolem en 1923. L’idée de départ est de tenter de définir une fonction calculable comme une fonction qui puisse être obtenue à partir de fonctions très simples et manifestement calculables par un processus récursif, c’est-à-dire un processus où la valeur prise par la fonction, lorsqu’on donne à la variable la valeur n+1, est reliée à la valeur de cette même fonction lorsqu’on donne à la variable la valeur n. Précisons cela : désignons par ℱn l’ensemble des applications de ℕn dans ℕ, où ℕ désigne l’ensemble des entiers naturels, par ℱ l’union de tous les ℱn, par s et σ les deux éléments de ℱ1 définis par s(n)=n+1, σ(n)=0 et par Pn,1,…,Pn, n les éléments de ℱn définis par Pn,k(m1,…mn)=mk. Soient f1,…,fk∈ℱm et g∈ℱk. Nous désignerons par g(f1⇑…⇑fk) l'élément de ℱm défini par g(f1⇑…⇑fk) (x)= g(f1(x),…,fk(x)) pour tout x∈ℕm.

Enfin, soient f∈ℱm et g∈ℱm+2. Nous désignerons par frekg l'élément de ℱm+1 défini par :

frekg(0,x)=f(x)

frekg(n+1,x)=g(n,frekg(n,x),x)

pour tout x∈ℕm.

Nous désignerons par 𝒫 et nous appellerons ensemble des fonctions primitives récursives le plus petit sous-ensemble de ℱ contenant s,σ,Pn,1…Pn,m pour tout n et stable par composition et par récursion. Plus précisément, si 𝒫n=𝒫∩ℱn, 𝒫 est le plus petit sous-ensemble de ℱ satisfaisant aux trois conditions :

  1. s,σ∈𝒫1, pour tout n∈ℕ,Pn,1…,Pm,n∈𝒫n ;
  2. f1,…,fk∈𝒫m,g∈𝒫k→g(f1⇑…⇑fk)∈𝒫m ;
  3. f∈𝒫m,g∈𝒫m+2→frekg∈𝒫m+1.

Nous avons construit ainsi un ensemble 𝒫 de fonctions méritant d'être appelées calculables.

Mais, dès 1928, Ackermann donne un exemple très simple de fonction méritant d'être appelée calculable et n’appartenant pas à 𝒫. Il s’agit de la fonction f∈ℱ2 définie par :

f(0,n)=n+1 ;

f(n+1,0)=f(n,1) ;

f(n+1,m+1)=f(n,f(n+1,m)).

C’est Gödel qui va parvenir, en 1934, en utilisant un projet de Herbrand à « agrandir suffisamment 𝒫 » pour parvenir enfin à une définition satisfaisante de la notion de calculabilité. Ce 𝒫 agrandi que nous désignerons par R et que l’on appelle ensemble des fonctions récursives générales se définit en permettant la génération de fonctions nouvelles non seulement par composition et par récursion mais aussi par minimalisation. Voici quelles sont des définitions précises : soit f∈ℱm+1. On désignera par μ(f) et on appellera minimalisation de f l’application de D dans ℕ définie par :

μ(f)(x)=min(n∈ℕ/f(n,x)=0) pour tout x∈D, D désignant le sous-ensemble de ℕm constitué par les x∈ℕm pour lesquels il existe un n∈ℕ tel que f(n,x)=0.

Il est facile de montrer que la fonction de Ackermann appartient à R.

En 1936, Church et Kleene introduisent la notion de λ-définissabilité. Church et Rosser démontrent peu après qu’elle est équivalente à la notion de fonction récursive et Church formule alors sa célèbre thèse : toutes les fonctions réputées intuitivement calculables ou, selon ses propres termes, « effectivement calculables » sont λ-définissables ou, ce qui est équivalent, récursives générales.

Il s’agit bien d’une thèse et non d’un théorème puisque son énoncé propose d’identifier un concept intuitif imprécis à un concept précis. Elle ne peut être démontrée mais peut être étayée par de nouvelles démonstrations d'équivalence.

Le premier pas décisif dans le renforcement de la thèse est accompli par Turing, en 1936, qui introduit une notion de machine qui est le résultat d’une analyse des opérations élémentaires qu’accomplit le conducteur d’algorithmes, peut-être stupide, mais fort obéissant dont nous avons déjà parlé. Presqu’en même temps, et indépendamment, Post décrit, en 1937,une machine analogue. La thèse que Turing énonce alors : toutes les fonctions réputées intuitivement calculables sont celles calculables par la « machine de Turing », apparaît équivalente à celle de Church puisque Turing lui-même démontre l'équivalence de son concept de calculabilité avec la λ-définissabilité. Le concept de machine de Turing est important car il a permis de définir exactement le concept d’algorithme sans passer par la gödelisation et a permis d'étendre à toute une série de problèmes (en particulier au problème des mots en théorie des groupes et au problème de la décidabilité des prédicats) la démonstration de l’impossibilité de résoudre le problème de Thue pour les demi-groupes qui avait été donnée par Post et Markov en 1947.

C’est Markov en 1951 qui donne une première définition du concept d’algorithme sans passer par la gödelisation. La thèse qu’il formule alors : tout algorithme au sens intuitif du terme peut s'écrire sous forme d’algorithme de Markov, est renforcée par Detlovsk qui démontre, en 1958, l’identité de l’ensemble des fonctions récursives et des fonctions calculables par un algorithme de Markov.

Markov est parvenu à sa notion d’algorithme en s’apercevant que les démonstrations, les calculs, les transformations logiques consistent essentiellement à transformer certains mots en d’autres suivant diverses règles. C’est dire que sa formulation vient s’inscrire tout naturellement dans le cadre très général formulé par Post en 1943 et qu’on désigne maintenant sous le nom de « calcul de Post ».

diagramme_notions

C’est également comme un cas très particulier de calcul de Post qu’apparaissent les grammaires de Chomsky en 1955. Elles fournissent un modèle fondamental pour l'étude non seulement des langues naturelles mais aussi des langages de programmation que d’autres conférenciers auront maintes fois l’occasion de définir et de développer dans leurs exposés.

1. Il est clair qu’il vaut mieux, pour la bonne conduite de l’algorithme, qu’un tel homme ne sache faire que cela et qu’un mathématicien aura quelque peine à oublier la signification des calculs qu’il effectue pour tenir convenablement un tel rôle pendant longtemps : le paysage le séduit trop. Ulysse se bouchait les oreilles pour ne pas entendre le chant des Sirènes !

Section : Informatique et technocratie

Dimanche 19 juillet 1970 (matin), intervention de Louis Pouzin, Délégation générale à l’informatique (pp. 429-435)

Intervention de Louis Pouzin

Peut-on être pour la technocratie ? Bien qu’il soit de bon ton d'être contre, n’est-ce pas un simple préjugé, d’autant plus mal fondé que l’on pourrait bien soi-même appartenir à une variété de technocrates retranchés dans l’informatique. Afin d’y voir plus clair, il paraît souhaitable de s’interroger sur ce que l’on entend par « technocrate ».

Peut-être pourrait-on déceler des traces du virus dans ces vocables nouveaux à effet certain tels que : techniques de la décision, préparation scientifique des décisions. Ce ne serait sans doute que colorations nouvelles plaquées sur des procédés anciens si le contexte n’impliquait le plus souvent l’utilisation d’ordinateurs. En d’autres termes, il y aurait là un phénomène nouveau dû à l'écrasante supériorité de la machine dans le domaine du traitement de l’information. Il semblerait, aux dires de certains, que l’on pourrait maintenant évaluer les conséquences des décisions de façon scientifique, quantifiée, objective, dénuée de tout facteur affectif, en compilant une masse suffisante d’information qu’aucun individu ne pourrait synthétiser par ses seuls moyens humains. Nous serions enfin bientôt débarrassés de ces décisions subjectives prises hâtivement sous la pression des circonstances. Mais pourquoi y aurait-il encore besoin de gens pour prendre ces décisions ? Si une machine est capable de produire le bilan quantitatif d’une alternative en traitant des masses considérables de données, on ne voit pas très bien ce qui empêcherait de pousser l’opération un pas plus avant et de produire la meilleure des alternatives. Si maintenant on prend une décision différente, c’est sans doute que la meilleure alternative était inapplicable, donc mal évaluée.

Est-ce là une attitude légitime de suspicion vis-à—vis du traitement mécanique de l’information ? Sert-il vraiment à quelque chose ? Ou bien ne jouons-nous pas la tragi-comédie de prendre des décisions dictées par des machines ?

De tout temps, les décisions ont été fondées notamment sur des « informations ». Tous les pouvoirs sécrètent des réseaux d’information, officiels ou non. Avec le temps et la conquête des libertés individuelles, les sociétés humaines ont développé des formes de pouvoir construites sur une collecte ouverte et organisée de l’information. C’est ce qu’on appelle une démocratie. Les opinions de chacun, recueillies au niveau le plus élémentaire, sont concentrées pour aboutir à une expression commune d’opinion générale. Sans être nécessairement partagée par tout le monde, elle devrait être au pire la moins mal partagée.

Il existe d’autres formes moins officielles de collecte d’information : les renseignements généraux, les services spéciaux, les études de marché, les sociétés de crédit, les gangs. Ces organisations collectent et traitent des informations par leurs moyens propres, afin de pouvoir prendre des décisions conformes à leurs intérêts particuliers. Une des techniques élémentaires du renseignement consiste à entourer de mystère ce que l’on sait réellement. La collecte d’information a donc le plus souvent lieu par des voies indirectes. Le processus n’est pas consultatif en ce sens que l’on n'éclaire pas 1e public sur les véritables facteurs que l’on désire connaître. Ceux-ci sont dissimulés soit par l’utilisation de moyens confidentiels, soit par des formes de collecte anonymes et peu explicatives. À quoi ou à qui servent, par exemple, les fiches de débarquement « obligatoires » que doit remplir tout passager français venant d’un aéroport étranger ? Le processus est également dénué d’aspect délibératif. Le public, n'étant pas informé de la véritable information recherchée, est encore moins convié à débattre du sujet.

On pourrait imaginer que tous ces réseaux d’information, occultes ou transparents, n’ont pour but que de rassembler le maximum d'éléments à partir desquels seraient évaluées des décisions judicieuses dans un environnement déterminé. Il n’est pas interdit de penser que cela se produise en effet. Mais il est différentes natures de décisions. Peut-on par exemple placer sur le même plan les mesures de dépannage d’un atelier après un incident technique, la fermeture d’une agence régionale d’une grande société, la fixation du taux d’intérêt de la Banque de France ou l’entrée de la Grande-Bretagne dans le marché commun ? La fermeture d’une agence régionale peut être la conséquence d’une opération de concentration de moyens. Elle peut aussi mettre en émoi des notables, des clients, des politiciens. Il est nécessaire de peser tous ces éléments avant d’en décider. Mais l’opération de concentration n’en est pas moins poursuivie, avec l’objectif de fermer un certain nombre d’agences. Les facteurs essentiels seraient très différents si l’agence était le seul établissement de la société.

Dans la pratique, les décisions sont prises à plusieurs niveaux, que l’on peut qualifier de stratégiques et tactiques. On pourrait dire aussi décision de pouvoir et de gestion, ou bien de politique et de logistique. Une décision prise à un niveau de pouvoir élevé ne peut être appliquée que par transformation en une cascade de décisions intermédiaires prises ultérieurement par un grand nombre de personnes. Traditionnellement, l’impossibilité pratique d'évaluer tous les facteurs pesant sur une décision de haut niveau conduit le plus souvent à décider d’abord, tenter d’appliquer ensuite. Si un réseau d’information est utile pour aider à prendre une décision de haut niveau, il est tout aussi apte à faciliter la prise des décisions subséquentes, qui sont les plus nombreuses, et d’autant plus ressenties par le public qu’elles atteignent un stade final d’application. Comme il existe souvent une multitude de voies pour aboutir à des objectifs généraux, les décisions intermédiaires ont surtout pour but de choisir des voies de moindre résistance. Un réseau d’information est alors un outil inséparable du pouvoir pour aboutir à la réalisation de ses objectifs.

L’information collectée et traitée par les seuls moyens humains est personnalisée. Les traits d’observation et de jugement des individus influent sur les résultats. La masse d’information est de plus limitée. En face de cela, un ordinateur peut absorber une quantité quasi-illimitée d’informations brutes. Il serait donc l’outil idéal pour remédier aux défauts inhérents aux moyens d’information humains, tant par sa puissance de synthèse que par son objectivité.

En réalité, une masse d’informations brutes est inutilisable, quelle que soit la manière d’additionner des faits élémentaires, car ils n’ont pas la même signification du point de vue de ce que l’on recherche. Pour obtenir des résultats utilisables, il faut traiter l’information, autrement dit utiliser des procédés d’analyse et de réduction des données qui les transforment selon des lois choisies avec plus ou moins de bonheur. Il peut apparaître à ce stade des distorsions involontaires ou non, conséquences d’erreurs techniques ou de coups de pouce délibérés. Il est courant de lire des résultats d'études donnant une pléthore de chiffres en apparence cohérente (la somme des pourcentages est 100) et qui ont la réputation de sortir des ordinateurs. On n’indique jamais de quelle manière ces résultats ont été obtenus. Ce serait d’ailleurs impraticable, car le traitement effectué peut être d’une telle complexité que sa compréhension est réservée aux seuls spécialistes.

L’ordinateur producteur d’information est communément crédité de cette neutralité qui fait tomber les passions et clôt les discussions. Or, le seul élément neutre se réduit à l’ordinateur. Les informations brutes ne sont pas neutres. Aussi nombreuses soient-elles, elles sont choisies parmi d’autres que l’on ne retient pas. Le traitement n’est pas neutre, c’est un programme qui reflète une méthode de certains experts. Les résultats ne sont pas neutres, car il est bien rare que l’on publie tout ce qu’il est possible d’obtenir. Mais l’ordinateur impavide sert de paravent commode. Il n’est plus possible de contester l’information dont personne n’est responsable. Tout au plus admet-on quelquefois une « erreur » d’ordinateur, autre paravent commode pour désigner une erreur humaine. Puisque les informations sont supposées neutres, cette qualité se transfère aussi aux décisions qui en découlent logiquement, disons fatalement. Il est humain d'être en désaccord avec des décisions prises par d’autres, et au besoin de s’en prendre aux auteurs. Si un pouvoir est jugé par trop contraignant, certaines personnes peuvent tenter de s’en saisir en en chassant d’autres. Prendre ou conserver le pouvoir sont des occupations qui impliquent nommément des individus. Faire passer l’ordinateur pour le véritable instrument de décision a pour effet de dépersonnaliser le pouvoir. C’est sans doute pour ceux qui le détiennent un moyen adroit de le conserver, car on ne voit pas très bien comment prendre un pouvoir qui n’est visiblement exercé par personne.

L’ordinateur paravent n’est pas seulement utile aux mains de ceux qui détiennent le pouvoir face à ceux qui ne l’ont pas. Habituellement, le pouvoir est en réalité un ensemble de clans, organismes, directions,… entre lesquels apparaissent des désaccords et des rivalités pour des positions plus dominantes. La connaissance des techniques informatiques est encore assez précaire dans les milieux dirigeants, dont la moyenne d'âge fait remonter la formation à une autre époque. Moyennant une présentation quelque peu différente, un homme de pouvoir est aussi neutralisé par des produits d’ordinateur qu’un homme sans pouvoir. À toutes fins utiles, il est prudent de s’entourer des meilleurs augures avant de prendre une décision comportant des risques. En cas d’ennui, la référence à l’ordinateur peut apporter des justifications ou échappatoires supplémentaires.

En résumé, l’informatique apporte de nouveaux instruments de pouvoir que nous ne savons pas encore bien utiliser ou neutraliser. Il se caractérisent par une présentation scientifique des informations et des décisions. La technicité et la dépersonnalisation apparentes des mécanismes utilisés les rend assez peu vulnérables à la contestation individuelle. La distinction entre les méthodes rigoureuses et les amalgames pseudo-scientifiques est encore assez peu perceptible dans la société actuelle, et le mythe de l’ordinateur se cultive aussi bien dans les milieux de pouvoir qu'à l’extérieur. L’invocation de l’ordinateur est un camouflage commode pour l’accomplissement de politiques occultes.

Sous la présidence de Mme Claudine Marenco, hormis les conférenciers, sont intervenus dans la discussion R. Cohen, F. Le Lionnais, R. Mesrine, J. Urvoy, J. Weinbach.